[CS 스터디] 5.1 시간복잡도와 공간복잡도

목차
1. 자료구조
💡 자료구조란?
: 효율적으로 데이터를 관리하고 수정, 삭제, 탐색, 저장할 수 있는 데이터의 집합
우리가 자료구조를 배우는 이유는 다음과 같다.
- 데이터를 체계적으로 저장하고, 효율적으로 활용할 수 있다.
- 자료구조를 알면 특정한 상황에 놓인 문제를 수월하게 해결할 수 있다.
[면접을 위한 CS 전공지식 노트] 는 C++ 기반의 자료구조를 다루고 있다.

2. 복잡도
좋은 알고리즘이란 실행 시간도 짧으면서 저장공간도 적게 쓰는 알고리즘이다. 하지만 두 가지를 다 만족하기는 어렵고, 시간과 공간은 대체적으로 반비례적인 경향이 있다. 최근에는 대용량 시스템이 보편화 됐으므로 프로그램을 구현할 때에는 공간복잡도보다는 시간복잡도가 우선이 된다.
2.1 시간 복잡도 (Time Complexity)
💡 시간 복잡도란?
: "문제를 해결하는 데 걸리는 시간과 입력의 함수 관계" 를 일컫는다.
보통 명령문의 실행 빈도수에 따라 대략적으로 소요 시간을 나타내기 위해 사용한다.
그렇다면 시간 복잡도는 왜 필요한가?
입력값이 적을 경우에는 크게 상관이 없지만, 시간 복잡도가 필요한 경우는 더 큰 데이터를 다룰 때이다. 입력값이 커질 수록 그에 비례하여 연산 횟수가 커지기 때문이다. 이 때 필요한 것이 시간 복잡도를 고려한 효율적인 알고리즘이다. 입력값이 커짐에 따라 증가하는 시간의 비율을 최소화한 알고리즘을 구성해야 한다.
어떠한 알고리즘의 로직이 '얼마나 오랜 시간'이 걸리는지를 나타내는 데 쓰이며, 보통 Big-O(빅-오) 표기법으로 나타낸다.
💡 Big-O(빅-오) 표기법 이란?
: 입력 범위 n을 기준으로 해서 로직이 몇 번 반복되는지 나타내는 것이다.
빅오 표기법은 상한 점근이므로 최악의 경우를 고려한다. 따라서 프로그램이 실행되는 과정에서 소요되는 최악의 시간까지 고려할 수 있다.
예를 들어 다음과 같은 식이 있다.
4n^2 + 3n + 21
O(n^2)빅오 표기법은 최악의 시간을 고려하므로 위의 예시는 최고차항인 n^2만을 표기하게 된다.
Big-O(빅-오) 표기법의 종류
| O(1) | 상수시간 입력의 크기와 상관 없이 항상 같은 시간이 걸리는 알고리즘 |
배열, 해시 테이블 |
| O(log n) | 로그시간 문제를 해결하는데 필요한 단계들이 연산마다 줄어드는 알고리즘 |
이진탐색, 힙 삽입/삭제 |
| O(n) | 선형시간 입력값이 증가됨에 따라 시간 또한 같은 비율로 증가하는 알고리즘 모든 입력값을 적어도 한 번 이상은 살펴봐야 한다. |
정렬되지 않은 리스트에서 최대값 최소값 탐색 |
| O(n log n) | 선형로그시간 데이터의 수가 2배로 늘 때, 연산 횟수는 2배 조금 넘게 증가한다. |
힙 정렬, 병합 정렬 |
| O(n^2) | 제곱시간 2중 반복을 도는 알고리즘 |
버블 정렬 |
| O(2^n) | 지수시간 입력값의 제곱만큼 증가하는 알고리즘 |
피보나치(재귀), 부분집합의 모든 경우의 수를 도출 |
| O(n!) | 팩토리얼 시간 빅오 중 가장 느린 알고리즘 |
순열의 모든 경우의 수 도출 |

O( 1) < O( log n) < O( n) < O( n log n ) < O( n²) < O( n³) < O( 2n ) < O( n! )
2.2 공간 복잡도(Space Compelxity)
💡 공간 복잡도란?
: 프로그램을 실행시켰을 때 필요한 자원 공간의 양을 일컫는다.
총 필요 저장 공간은 고정 공간과 가변 공간으로 구분된다.
- 고정 공간(알고리즘과 무관한 공간)
: 코드 저장 공간, 단순 변수 및 상수 - 가변 공간(알고리즘 실행시 필요한 공간)
: 실행 중 동적으로 필요한 공간
공간 복잡도는 다음과 같이 계산한다.
S(P) = c + Sp(n)c : 고정 공간
𝑆𝑝(𝑛) : 가변 공간
고정 공간은 상수이므로 공간 복잡도는 가변 공간에 좌우된다.
2.3 자료구조에서의 시간 복잡도

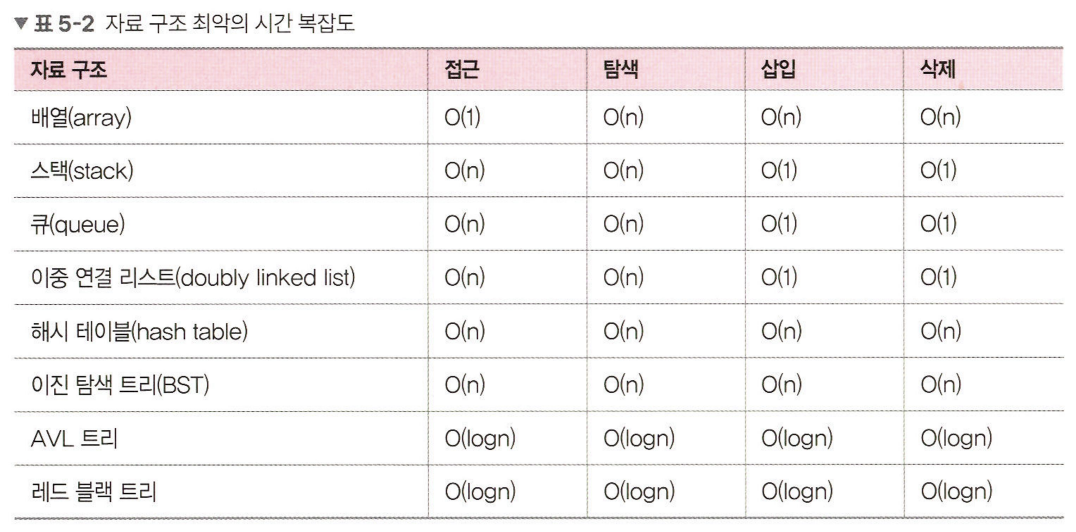
[참고]
https://insight-bgh.tistory.com/506
https://codermun-log.tistory.com/235
https://hudi.blog/time-complexity/
